True Vertical Depth
In near-vertical wells, we can be reasonably sure of the depth to a particular formation. In deviated wells, we need to calculate true vertical depth to that formation AND place the location where the wellbore intersects the reservoir. The results of this calculation allow us to correctly position reservoirs on geological sections, contour maps, and 3-D visualizations.

True vertical depth is a tricky business because six methods have been used over the years. The results vary in accuracy depending on how crooked the borehole is and how closely spaced the survey points are positioned. For a relatively straight deviated well, the tangential method is easy and quite adequate. For a well with many twists and turns, and for horizontal wells, more sophisticated methods are needed. The minimum curvature method seems to be the most popular.

Directional surveys measure wellbore deviation from the vertical and wellbore direction (azimuth) corrected to true North. Typical directional surveys are run inside drill pipe, with data measured every time a new drill pipe stand is readied for use - this occurs every 100 feet (30 meters) give or take a bit. Older surveys mau have much longer or erratic spacings between measurements.

With the increased use of horizontal wells in many reservoirs, the accurate representation of the wellbore trajectory between measurement stations has become important, for both practical and legal reasons. The math for this is a little beyond the scope of this Handbook. Click HERE for a description of a Visual Basic assisted spreadsheet for this purpose. THIS CHAPTER "A Compendlum of Directional Calculations Based on the Minimum Curvature Method", S.J. Sawaryn and I. L. Thorogood, SPE 84246, 2003.

Real-time continuous logging while drilling directional surveys minimize the calculation problem while geo-steering directional or horizontal wells. Continuous directional data from dipmeters, image logs, and other open hole well logs also give accurate results, but of course are "after the fact" and cannot help with geo-steering. A virtue of well logging methods is the ability to log data inbound and outbound, making for a "closed" survey in which accumulated closure errors can be distributed around the entire data set. This cannot be done in conventional station by station surveys.

CAUTION: If you write your own spreadsheets to run these calculations, note that the default units for angles is RADIANS and not degrees. The math below assumes angles are in degrees except where noted in Method 6.

Tangential Method
The tangential method uses only the inclination and direction angles measured at the lower end of the survey course length. The well bore path is assumed to be a straight line throughout the course. This method has probably been used more than any other and is the least accurate. It makes the well appear too shallow and the lateral displacement too large. In a typical deviated well, the true vertical depth can be wrong by more than 50 feet.

It has been used and perpetuated because of its inherent simplicity of hand calculation. Calculating the survey by the tangential method, however, is no longer justifiable because programmable calculators and field portable computers make the better methods just as easy as this one. This method is not recommended any time in any well. However, many such surveys are in the well files and many true vertical depths have been used, and may still be accepted, based on this erroneous data. All that is needed for a re-computation using better methods is the raw inclination and direction data, and this is usually available. Re-computation is strongly recommended.

If surveys were taken at approximately 1 ft. intervals, the error would be tolerable, but this frequency cannot be economically justified with typical single shot surveys. However, this frequency of measurement is achieved with continuous directional surveys run with the dipmeter. If computations are made at short intervals, then the tangential method works fine. Most station by station surveys are taken at much larger intervals, such as a few to several hundred feet apart, and therefore the results are inaccurate. If the dipmeter program calculates vertical depth at similar intervals, it is also inadequate.

The formula are:
      1: North = SUM ((MD2 - MD1) * Sin WD2 * Cos HAZ2)
      2: East = SUM ((MD2 - MD1) * Sin WD2 * Sin HAZ2)
      3: TVD = SUM ((MD2 - MD1) * Cos WD2)

NOTE: This is the high tangential method. If WD1 and HAZ1 replace WD2 and HAZ2, it is the low tangential method.

Where:
  East = easterly displacement (feet or meters) - negative = West
  HAZ1 = hole azimuth at top of course (degrees)
  HAZ2 = hole azimuth at bottom of course (degrees)
  MD1 = measured depth at top of course (feet or meters)
  MD2 = measured depth at bottom of course (feet or meters)
  North = northerly displacement (feet or meters) - negative = South
  TVD = true vertical depth (feet or meters)
  WD1 = well deviation at top of course (degrees)
  WD2 = well deviation at bottom of course (degrees)

Average Tangential Method
The angle averaging method uses the angles measured at both the top and bottom of the course length in such a fashion that the simple average of the two sets of measured angles is assumed to be the inclination and the direction. The wellbore then is calculated tangentially using these two average angles over the course length. This method is a very simple, and more accurate, means of calculating a wellbore survey.
      1: North = SUM ((MD2 - MD1) * Sin ((WD2 + WD1) / 2) * Cos ((HAZ2 + HAZ1) / 2))
      2: East = SUM ((MD2 - MD1) * Sin ((WD2 + WD1) / 2) * Sin ((HAZ2 + HAZ1) / 2))
      3: TVD = SUM ((MD2 - MD1) * Cos ((WD2 + WD1) / 2))

Balanced Tangential Method
The balanced tangential method uses the inclination and direction angles at the top and bottom of the course length to tangentially balance the two sets of measured angles. This method combines the trigonometric functions to provide the average inclination and direction angles which are used in standard computational procedures. The values of the inclination at WD2 and WD1 are combined in the proper sine-cosine functions and averaged. This method did not lend itself to hand calculations in the early days, but modern programmable scientific calculators make the job easy.

This technique provides a smoother curve which should more closely approximate the actual wellbore between surveys. The longer the distance between survey stations, the greater the possibility of error. The formula are:
      1: North = SUM (MD2 - MD1) * ((Sin WD1 * Cos HAZ1 + Sin WD2 * Cos HAZ2) / 2)
      2: East = SUM (MD2 - MD1) * ((Sin WD1 * Sin HAZ1 + Sin WD2 * Sin HAZ2) / 2)
      3: TVD = SUM ((MD2 - MD1) * (Cos WD2 + Cos WD1) / 2)

Mercury Method
The mercury method is a combination of the tangential and the balanced tangential method that treats that portion of the measured course defined by the length of the measuring tool in a straight line (tangentially) and the remainder of the measured course in a balanced tangential manner. The name of the mercury method originated from its common usage at the Mercury, Nevada test site by the US Government.
      1: North = SUM ((MD2 - MD1 - STL)*((Sin WD1 * Cos HAZ1 + Sin WD2 * Cos HAZ2)/2)
                   + STL * Sin WD2 * Cos HAZ2)
      2: East = SUM ((MD2 - MD1 - STL) * ((Sin WD1 * Sin HAZ1 + Sin WD2 * Sin HAZ2) / 2)
                 + STL * Sin WD2 * Sin HAZ2)
      3: TVD = SUM (((MD2 - MD1 - STL) * (Cos WD2 + Cos WD1) / 2) + STL * Cos HAZ2)

Where:
  STL is the length of the survey tool

Radius of Curvature Method
The radius of curvature method uses sets of angles measured at the top and bottom of the course length to generate a space curve (representing the wellbore path) that has the shape of a spherical arc passing through the measured angles at both the upper and lower ends of the measured course. This method is one of the more accurate means of determining the position of a wellbore when survey spacing is sparse. The assumption that the wellbore is a smooth curve between surveys makes this method less sensitive to placement and distances between the survey points than other methods.

CAUTION: It is a terrible method when data is closely spaced, as the subtractions in the equation create either "divide by zero errors" or an incorrect TVD when the borehole is a straight line but deviated.
      1: North = SUM (MD2 - MD1) * (Cos WD1 - Cos WD2) * (Sin HAZ2 - Sin HAZ1)
                   / ((WD2 - WD1) * (HAZ2 - HAZ1))
      2: East = SUM (MD2 - MD1) * (Cos WD1 - Cos WD2) * (Cos HAZ1 - Cos HAZ2)
                 / ((WD2 - WD1) * (HAZ2 - HAZ1)}
      3: TVD = SUM (MD2 - MD1) * (Sin WD2 - Sin WD1) / (WD2 - WD1)

Minimum Curvature Method
The minimum curvature method, like the radius of curvature method, takes the space vectors defined by inclination and direction measurements and smoothes these onto the wellbore curve by the use of a ratio factor which is defined by the curvature (dog-leg) of the wellbore section. The method produces a circular arc as does the radius of the curvature. This is not, however, an assumption of the method, but a result of minimizing the total curvature within the physical constraints on a section of wellbore.
      1: DL = Arccos (Cos (WD2 - WD1) - Sin WD1 * Sin WD2 * (1 - Cos (HAZ2 - HAZ1)))
      2: CF = 2 / DL * (Tan (DL / 2)) * 0.017 453
      3: North = SUM ((MD2 - MD1)*((Sin WD1 * Cos HAZ1 + Sin WD2 * Cos HAZ2) / 2) * CF)
      4: East = SUM ((MD2 - MD1) * ((Sin WD1 * Sin HAZ1 + Sin WD2 * Sin HAZ2) / 2) * CF)
      5: TVD = SUM (((MD2 - MD1) * (Cos WD2 + Cos WD1) / 2) * CF)

Where:
  DL = dog leg severity (degrees)
  CF = curvature factor (radians)

The term  0.017 453 converts degrees to radians.

META/LOG "TVD" SPREADSHEET -- True Vertical Depth
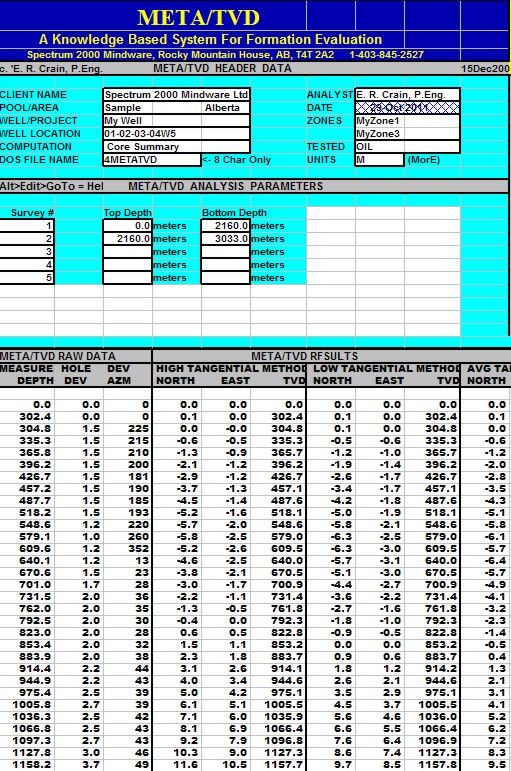
This spreadsheet calculates True Vertical Depth from seven common methods. The more exotic methods are more accurate and there is no excuse for not using them, since the spreadsheet does all the hard work.

SPR-23 META/LOG TRUE VERTICAL DEPTH (TVD) CALCULATOR
 Calculate true vertical depth TVD, X aand Y coordinates,  7 methods.
 

///////                 //////            ///////             //////             ///////        //////


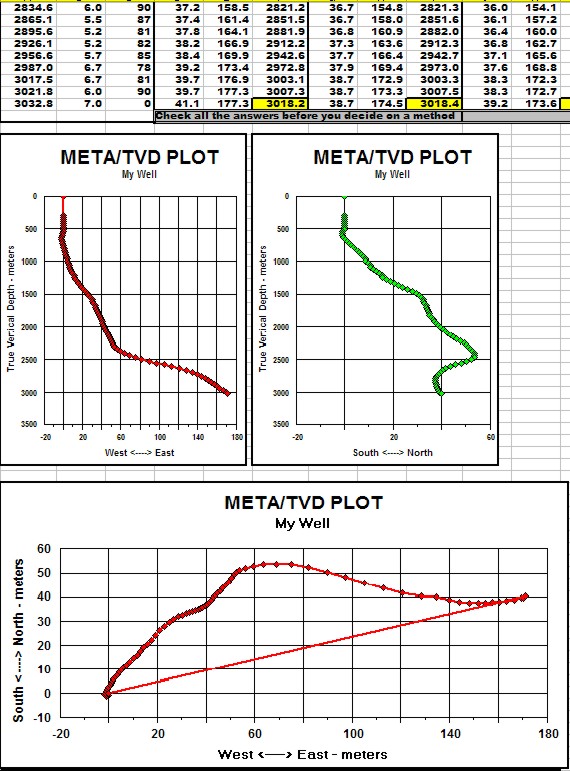
Sample output from META/LOG "TVD" Spreadsheet -several more sets of results are offscreen to the right.