High Resolution Dipmeter
Four and six arm tools are less vulnerable to hole problems than 3-arm tools. These are called high resolution dipmeters. If one curve is unusable, any three others may still be used to determine dip. Also, the two (or three) independent sets of arms fit elliptical holes better. For these reasons, four and six arm tools became the preferred dipmeter in the 1970's and 80's.

Six curve pair correlations can be attempted between four curves. The adjacent curve pair displacements are designated respectively as h12, h23, h34, and h41, and the diagonal displacements as h13 and h24. These six displacements can in turn be paired in thirteen different ways to provide thirteen dip evaluations for the same level. For the six arm dipmeter, 15 pairs are possible, leading to additional redundancy. The result from each combination is referred to as a dip determination. In recent practice, however, only four or five correlations are made, leading to a maximum of eight possible dip determinations per level. This reduces computer time.

Four arm closure error (Ec) is given by the algebraic sum of the four adjacent curve displacements:
      1: Ec = h12 + h23 + h34 + h41

For perfect closure, Ec = 0.

Three arm closure error can also be computed on a four arm or six arm dipmeter. In this case, closure error is given by the algebraic sum of two adjacent curve displacements and their associated diagonal displacement. This error is distributed around the displacements in proportion to the amount of each displacement.

When four or six arm closure exists, or has been created by distributing the error, another error, the planarity error can be measured among the four adjacent curve displacements. Because opposite pairs of pads in the four pad array form a parallelogram, the displacement observed between curves 1 and 2 should be the same as that between curves 4 and 3, and the displacement between curves 2 and 3 should be equal to that between curves 1 and 4. Thus, for perfect planarity:
      2: h12 = -h34 and h23 = -h41

When four arm closure error is zero, planarity error (Ep) is defined as:
      3: Ep = h12 + h34 - h23 - h41

For perfect planarity, Ep = 0. Similar equations exist for the six arm dipmeter.

If closure error is zero and planarity is not zero, then several things may be possible. One is that the bedding may not be planar, such as in the case of festoon current bedding or aeolian dune surfaces. Other possibilities are lack of pad contact with the hole wall and possible miscorrelations. The latter are,
in fact, quite likely.

The flow chart below shows the complex logic involved in Schlumberger's high resolution dipmeter program. It handles the closure and planarity problems in numerous ways, based on the number and quality of correlations found.

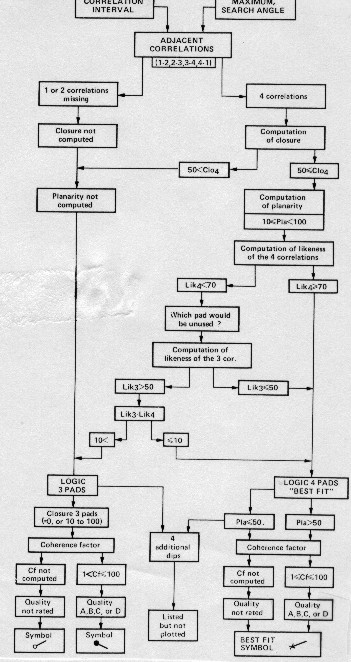
Dipmeter computation flowchart

The output listing from this program is shown below. Notice that some of the logic choices are coded on the listing and others on the arrow plot by use of alternate symbols.

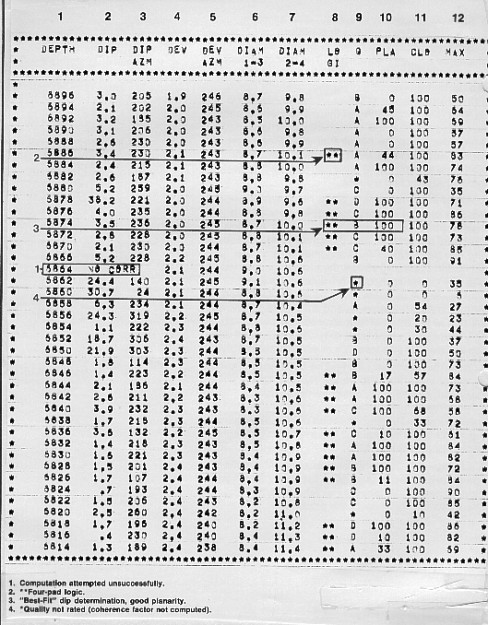
SHDT dipmeter computation output listing

Dips can also be coded and presented in such a way as to indicate the fact that they are non-planar. This would help an analyst interpret the bedding, as shown in the example below, which was processed using Gearhart's OMNIDIP program.

Coding non-planar dips helps interpret sedimentary bedding