Permeability from STONELEY WAVE
 This method is reproduced from a Schlumberger petrophysical analysis report, edited fpr clarity and consistency with "computer-ready" math concepts. The method relies on the presence of a Stoneley wave travel time curve from a dipole shear or array sonic (full waveform) acoustic log.

Stoneley waves are dispersive (velocity varies with frequency), and are generated from the interaction between borehole and formation. At low frequency, it is called a tube-wave. A Stoneley waveform has a frequency content of 0.1 to 3 KHz, with most of the energy in the late arrivals at about 500 Hz.

Stoneley waves are usually detected between 0 to 20 ms on the sonic waveform. In contrast, the shear waveforms are usually detected between 0 to 5 ms and are concentrated around 4 KHz.

The Stoneley slowness increases due to fluid movement in porous media and mud cake around the borehole. The mud cake effect on slowness is usually a constant shift if the mud cake thickness is constant and if the mud is of one type. One of the major factors affecting Stoneley slowness is grain modulus. If the lithology is changing from pure calcite to dolomite or to more siliciclastic, the effect on slowness will vary. In addition, Stoneley wave is affected by pore fluid modulus. For instance, if fluid is changing from liquid to gas, the predicted permeability increases by two decades.

Stoneley wave is affected by porous media fluid and by shear modulus at low frequency. Stoneley wave slowness can be modeled in non-permeable zones as follows:
      1: DTST^2 = (DENSfluidf * DTS^2 / DENS) + DTCfluid^2

Where:
  DTST = stoneley slowness (μs/ft)
  DTS = shear slowness (μs/ft)
  DENS = bulk density (g/cc)
       calculated from probabilistic analysis  by summing the density contriburion from all minerals and fluids
  DENSfluid = mud filtrate sensity (g/cc)
  DTCfluid = mud filtrate slowness (μs/ft)

By cross-plotting DTST^2 versus DTS^2 / DENS across a zero permeability zone, the slope of the straight line is DENSfluid and Y-intercept is DTCfluid^2. There is one condition on the linear fit:  all data on thecross plot should be above or on the fitted line.

The Stoneley permeability index is estimated by taking the ratio of actual measured Stoneley slowness and modeled slowness as per above model. The formula can be written as follows:
      2: STI = DTST / (((DENSfluid * DTS^2 / DENS) + DTCfluid^2)^0.5)

Where:
  STI = Permeability index from Stoneley wave travel time (fractional  - range = 0 to 1)

Flow Zone Index (FZI)
 This STI model is still affected by  variations in mud cake and formation fluid type. In addition, it does not provide a means to estimate mobility or permeability magnitude directly.

Stoneley permeability index is not a permeability estimation, but it is an index of fluid movement in porous media around the borehole. Since fluid movement is a function of pore throat distribution, pore shape, and pore size, the Stoneley permeability index is a tortuosity index only. These factors can be combined in a concept called Flow Zone Index (FZI).

The Stoneley permeability index Kist is a direct measurement of FZI. Since FZI approaches to zero when Stoneley permeability index approaches to 1 in non-permeable zones, and both of them approach to infinity when permeability approaches to infinity, then a simple relationship can be derived between FZI and STI as following:
      3: FZI = IMF * (STI – 1)

Where:
  FZI = flow zone index
  IMF = flow zone index matching factor

With this equation, the only empirical factor to match actual permeability profile is IMF. Since the grain modulus has an effect on Stoneley slowness, IMF can be computed in  the probabilistic model by summing the volume weighted IMF for eaach individual mineral in the model. Note: the Schlumberger report does not indicate how the individual IMF parameters were derived. Values quoted were:
  Zone "A" Calcite = 12, Illite = 0.001, Kaolinite = 0.001, Quartz = 1.0, Siderite = 0.0
  Zone "B" Calcite = 10, Illite = 0.001, Kaolinite = 0.001, Quartz = 130, Siderite = 0.0

Stoneley permeability can be computed by using effective porosity and FZI with the following: equations:
    4: PERMst = MPERM * FZI^2 * (PHIe^3 / (1- PHIe)^2)

Where:
  PERMst = permeability from Stonely method (md)
  PHIe = effective porosity
  FZI = flow zone index
  MPERM = permeability calibration factor (default = 1014)

This method is valid for the following conditions:

• Single-phase fluid in porous media.
• Negligible temperature variation.
• Single type mud cake with fairly constant mud cake thickness.
• Sufficient logs for volumetric lithology modeling.
• Available core, MDT permeabilities or down-hole production profile with constant draw down.
• In bad holes or severely rough surface condition, this method is not valid any more.

This method is limited to the DSI vertical resolution of 3.5 ft. The volume measured by the DSI is 0.5 to 1 ft thick with 3.5 ft long cylinder.


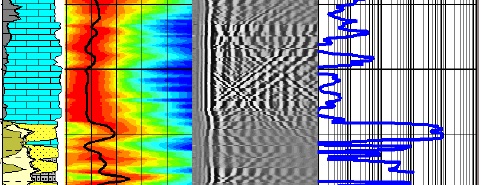
Example of permeability calculated from Stoneley wave travel time. Lithology (Track 1), Stoneley travel time (Track 2), VDL display (chevron patterns = fractures), calculated permeability - nilliDarcies (Track 5).
 
Page Views ---- Since 01 Jan 2015
Copyright 2023 by Accessible Petrophysics Ltd.
 CPH Logo, "CPH", "CPH Gold Member", "CPH Platinum Member", "Crain's Rules", "Meta/Log", "Computer-Ready-Math", "Petro/Fusion Scripts" are Trademarks of the Author