Dipmeter Calculations With Stereonets
The stereonet is an old, traditional tool for dipmeter analysis that has become unconventional by the passage of time. Developed before the days of calculators and computers, it allowed computation of many complex tasks that were tedious to perform by hand. Numerous software packages are available now to plot this data more neatly than can be achieved with pencil and paper.

These tasks include finding the projection of a plane, direction of a line normal to a plane, the line of intersection of two planes, angles between two planes, true dip from two apparent dips and vice versa, and regional dip removal. Some of these functions have been described earlier, using the calculator, SCAT, or tangent diagrams. Some people still prefer the stereonet, but the calculator is easier.

These instructions are paraphrased from "Schlumberger Dipmeter Fundamentals 1981", and the stereonets are copied from the previous edition dated 1970. For working through stereographic problems you should have a stereonet such as the one shown below, plus pieces of tracing paper large enough to cover it, or a plastic overlay, made from a xerographic reproduction of the next illustration. These two illustrations are used for high angle dips. Enlarged versions of the central portions of the illustrations are used for low angle dips (see below).

 

Stereonet for high angle dip

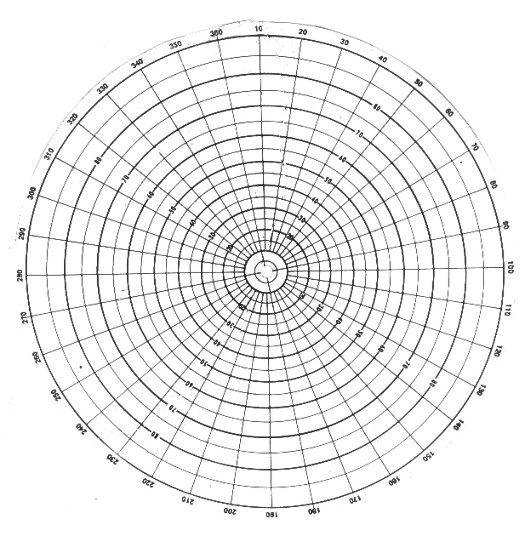
Stereonet overlay for high angle dip (reproduce on clear film)

Stereonet for low angle dip

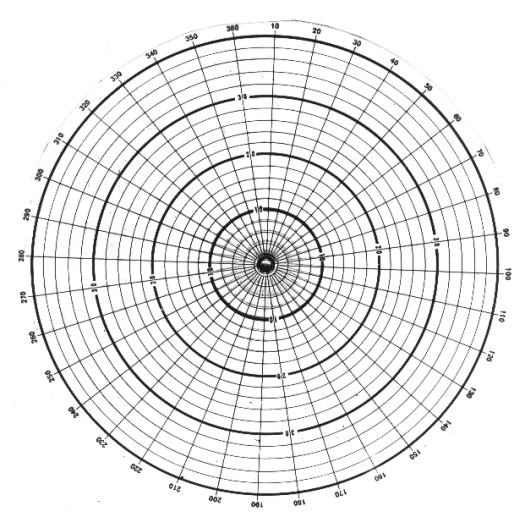
Stereonet overlay for low angle dip (reproduce on clear film)

The data for each problem are plotted on the tracing paper or overlay, and the stereonet is rotated to suit the differing orientations met with in each case. Although it is usually more convenient to lay the stereonet down and keep it fixed, while rotating the tracing paper over it, keep in mind that it is the tracing paper overlay, and not the net, that represents the fixed Earth.

If you use tracing paper, trace the outer circle of the stereonet on it and mark a "north" point with an N on the circle at some arbitrary point. Tracing the outer circle is necessary so that the two diagrams - overlay and stereonet - can be kept concentric in all orientations. You could achieve the same result by pinning the two layers together so that the tracing paper rotates about the center point of the stereonet. No matter how the overlay is rotated, the N point should be regarded as always pointing north.

If you use a transparent copy of the overlay, the circle and north point (0/360 degrees) are already marked. Use a grease pencil to mark points and lines, so it can be wiped off before the next example.

To understand how a stereogram is constructed, imagine standing on level ground and looking down into a hemisphere contoured at our feet and extending down into the ground, as if the ground were transparent. Any plane that passes through the center of a sphere cuts the spherical surface in an arc called a great circle. If we stand on an outcrop of a bed dipping down into the ground, we can imagine that the bed cuts the underground hemisphere with an arc of a great circle, below, top right.

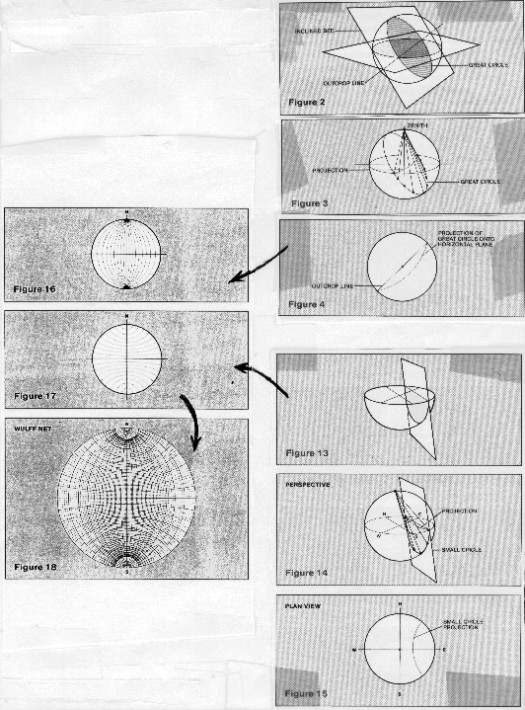
Stereonet - basic concepts

To project that circle up to the horizontal surface at ground level, we connect every point on the great circle to the zenith point of the sphere, above our head. The intersection of the lines with the horizontal plane form a new circle; many such circles form the north south grid lines of the stereonet, see above, middle left.

The intersections of vertical planes that do not pass through the center of the sphere intersect the hemisphere surface as small circles and can be projected up to the stereogram surface, via the zenith point, exactly as before, see above, lower right. These form the circles that are centered on the north and south poles, forming the east west grid on the stereonet. Superposition of the two sets of circles creates the final stereonet presentation, see above, lower left.

A straight line passing downward at a slant through the point at which we are standing cuts the hemisphere at a point that can be projected onto the stereogram by the same technique. Again, the zenith point provides the reference for the projection, see below, top right. Both lines and planes can be plotted on the same diagram, see below, middle right. Horizontal and vertical planes are special cases; the projection of a horizontal plane is the outer edge of the stereonet, a vertical plane passing through the center is a straight line, below, lower right.

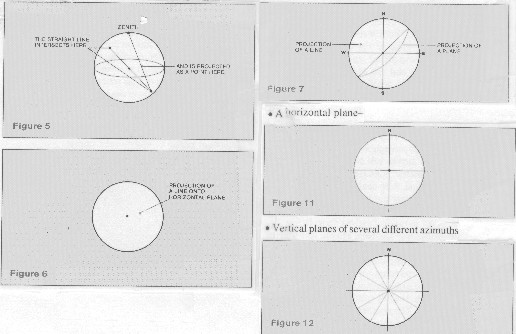
 Lines and planes on the stereonet

Illustrated below at upper left is how to plot the projection of a plane dipping 20 degrees in a N 40 degrees E direction:
   1. trace the outer circle of the stereonet onto the overlay and mark a "north" point on it. It helps to add the other cardinal points and the center.
   2. find N 40 degrees E on the edge of the stereonet and mark this point on the overlay. A line drawn between this point and the center represents the direction of dip of the plane.
   3. find a great circle appropriate to a dip in this direction by rotating the overlay until the N 40 degree E dip line lies along the east-west diameter. It doesn't matter whether you choose to point the dip line toward the east or the west, because we are going to return it to its rightful orientation later.
   4. now trace in the great circle arc corresponding to 20 degrees of dip. The outer circle of the stereonet represents zero dip, so count the 20 degrees inwards from the edge. Do not use the dip angles marked on the overlay - they count degrees in the opposite direction.
   5. finally, rotate the overlay back to bring north to the top. The curve on the overlay now represents the great circle which describes a dip of North 40 degrees East.

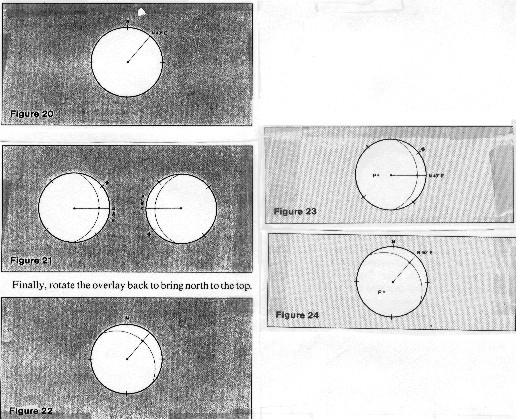
Projection of a plane

Lower right shows how to plot the direction of the line normal to the surface of the plane in example 1.
   1. rotate the overlay on the stereonet to place the dip line onto the east-west axis.
   2. the normal to a plane makes a 90 degree angle to the plane in all directions; therefore count 90 degrees from the great circle projection along the east-west diameter and mark point P.

Note that it doesn't matter in which direction you count along the diameter; if you should choose the direction that brings you to the edge of the net before reaching 90 degrees, jump to the other end of the diameter and finish counting from there. Check that both directions bring you to point P.

    3. rotate the overlay back to the position with north at the top, and check that point P lies in the southwest quadrant, as you would expect.
   4. this point, which represents the direction of the line normal to the given plane, is called the "pole" of the plane.

The image below, upper left, shows how to find the line of intersection of two planes: Given: plane A dips 20 degrees toward N 40 degrees E (the plane in example 1). plane B dips 30 degrees towards N 20 degrees W.
   1. plot the projections of these planes on the stereonet as in example 1.
   2. point P is the point of intersection of these two curves, and it therefore represents the projection of the line of intersection.
   3. rotate the overlay to bring point P to the north-south diameter of the stereonet, and read off its bearings. Count inward from the edge to find the dip angle and observe the direction along the edge of the stereonet. The line of intersection dips about 19 3/4 degrees in a direction 31 degrees east of north.

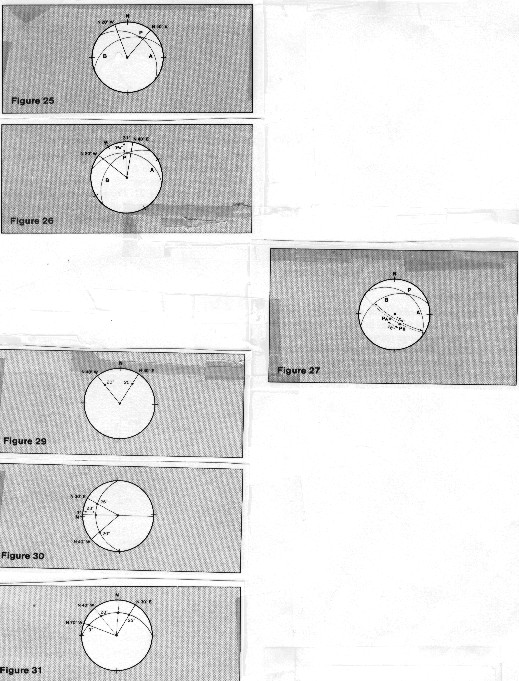
Line of intersection of two planes

Middle right, above, shows how to find the angle between the two planes in the previous example. Given: plane A dips 20 degrees toward N 40 degrees E (the plane in example 1). plane B dips 30 degrees towards N 20 degrees W.
   1. find the poles of the two intersecting planes (PA and PB), and also the great circle for which the point of intersection, P, is the pole. Notice that PA and PB both lie on this great circle, which follows from the fact that the plane normal to the line of intersection must also be perpendicular to both the given planes. Hence their poles lie on its great circle when plotted on the stereonet.
   2. find the dihedral angle between the planes, by either:
      a. measure the angle between PA and PB, or
      b. measure the angle between the original planes directly, using the third great circle as the measurement path.

Both methods should give the same answers, of course. Notice, however, that with the first method the angle measured directly between PA and PB is 26 degrees, while the angle between the great-circle arcs is 154 degrees. Because 26 degrees + 154 degrees = 180 degrees, we know that 26 degrees is the acute dihedral angle and 154 degrees is the obtuse dihedral angle between the given planes.

The bottom left illustration shows how to find true dip from dip measured in two different vertical planes: Given: dip A is 25 degrees, in a plane N 30 degrees E and dip B is 20 degrees, in a plane N 40 degrees W
   1. plot these measured dips on the stereonet.
   2. rotate the overlay until you find, by trial, the position for which these two points lie on the same great circle, and trace in that great circle arc.
   3. true dip angle and azimuth, 28 degrees at N 3 degrees E, can then be read directly from the stereonet.

Notice that this procedure can be worked backwards, to find the slope of a bed on any azimuthal direction if the true dip is known. First trace in the great circle for the bedding plane, knowing its dip; then find where this arc cuts a radial line drawn with the desired azimuth. You would need to do this twice to find transverse and longitudinal dip components.

If an inclined formation contains smaller bedded units within it, the computed dips of the subunits need to be corrected, by subtraction of the dip of the major system, to find their dips at the time of deposition. For the stereonet, the problem is that of rotating one plane by an amount, and in a direction, given by the dip of the other.

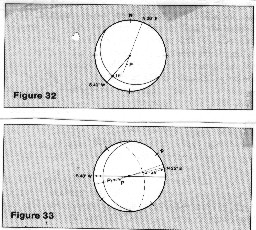The image at the right shows how to eliminate structural dip from computed dip. Given: formation dip of 30 degrees, azimuth N 20 degrees E structural dip of 15 degrees, S 40 degrees W
   1. plot the plane of the regional dip and add P, the pole of the formation dip.
   2. rotate the structural plane to the horizontal by moving its projection until it lies entirely on the outer circle of the stereonet.
   3. rotate the other plane through the same angle, which means moving its pole, point P, across the stereonet by the same distance and in the same direction as we move the projection of the structural plane. Be careful to measure "distance" in degrees and use the small circle arcs as guides to direction. So when the major plane rotates 15 degrees back to the horizontal, point P must move 15 degrees along a small circle arc to position P1.
   4. the dip of the sedimentary unit at the time of deposition was 46 degrees, azimuth N 25 degrees