Analyzing Dipmeters with Tangent Diagrams
Some structural analysis problems are easier to visualize when transformed into a single two dimensional domain instead of several, as arrow and SCAT plots do. The two methods available are tangent diagrams and stereonets. Tangent diagrams were described very well by C.A. Bengtson in Geology Vol 8 No 12 (1980) in "Structural Uses of Tangent Diagrams", reprinted in Geobyte, Mar 1989, along with an interactive computer program written by Robert Elphick.

Tangent diagrams, such as the example shown below, are special polar coordinate graphs that provide convenient graphic solutions for many problems of structural geology. Direction of dip is read at the circumference, and angle of dip is read from the concentric circles. The radius of each circle is proportional to the tangent of the angle of dip. High dips, therefore, plot farther from the center than low dips. The distinctive feature of this method of display is that planes can be represented by vectors, in a manner similar to stereonets, although tangent diagrams are more easily applied than stereonets.






 

Polar plot for tangent diagram

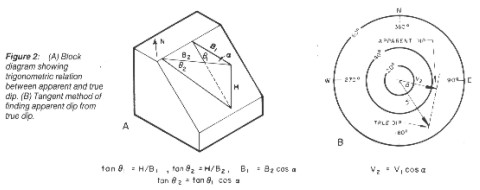
Shown below is a block diagram of a sloping plane, illustrates the basic principle of the tangent diagram. Line B1 is a horizontal line in the direction of true dip, and B2 is another horizontal line making an angle with B1. The trigonometric relations on this drawing demonstrate that the tangent of apparent dip in any direction is equal to the tangent of the true dip times the cosine of the angle between the directions of true dip and apparent dip.

Tangent diagram for homocline

The problem of finding apparent dip from true dip can be resolved vectorially on a tangent diagram, shown at right, below:
   1. plot V1, the true dip, as a vector from the origin with length proportional to the tangent of the angle of dip.
   2. draw a line V2 in the direction of the apparent dip.
   3. from the end of V1, draw a line perpendicular to V2.
   4. read the apparent dip from the intersection of the two lines.

Tangent diagrams for finding true dip and strike of folds

The illustration at top left shows how the tangent diagram is used to find true dip from two apparent dips:
   1. plot V1 and V2, the two apparent dips.
   2. draw perpendicular lines through their end points.
   3. read the true dip, V3, from the intersection of the perpendicular lines.

If two planes intersect, they have equal apparent dips in the vertical plane containing their line of intersection. The illustration at top right shows how this principle is used to find the line of intersection of two planes.
   1. plot V1 and V2, the true dip vectors of the two planes.
   2. connect the end points of the two vectors with a straight line.
   3. draw V3, the perpendicular from the origin to the straight line. This vector gives the bearing and plunge of the line of intersection of the two planes.

The lines of intersection of planes tangent to the bedding on the same or opposite flanks of an ideal cylindrical fold are parallel to the crestal line. Dip measurements obtained at random locations on such a structure will fall on a straight line when plotted on tangent diagrams, as exemplified by the dashed line in in the middle illustration above. The line for non-plunging folds passes through the center of the plot, plunging folds to one side (bottom illustration). Cylindrical folds plot as straight lines and conical folds as curved lines (see below).

More tangent diagrams for folds