Lithology fRom SONIC, DENSITY, NEUTRON, PE LOGS
One method of numerically evaluating lithology is to use the Mlith-Nlith method, which uses two formulae nearly independent of the porosity of the rock. The input data to these algorithms must be shale corrected, must be in limestone porosity units, and must be in English units before processing begins. Various 2 and 3 mineral models can be constructed from the available data - all possible combinations are listed in this Chapter.

Lithology fRom Mlith-Nlith Methods
Shale correct all data:
      1: PHIdc = PHID - Vsh * PHIDSH
      2: PHInc = PHIN - Vsh * PHINSH
      3: PHIsc = (DTC - (1 - Vsh) * 47.3 - Vsh * DTCSH) / (188 - 47.3)
      4: DENSc = PHIdc + (1 - PHIdc) * 2.71
      5: DTCc = PHIsc * 188 + (1 - PHIsc) * 47.3

Calculate Mlith and Nlith
      6: Nlith = (1.00 - PHInc) / (DENSc - DENSW)
      7: Mlith = 0.01 * (DTCW - DTCc) / (DENSc - DENSW)

2-Mineral Model Using Mlith
If the usual lithology is made up of two minerals, then the Mlith and Nlith values can each be linearly interpolated to find the fraction of the minerals.
      8: Vmin1 = (Mlith - MLITH2) / (MLITH1 - MLITH2)
      9: Vmin2 = 1.00 - Vmin1

2-Mineral Model Using Nlith
      10: Vmin1 = (Nlith - NLITH2) / (NLITH1 - NLITH2)
      11: Vmin2 = 1.00 - Vmin1

3-Mineral Model Using Mlith and Nlith
If the usual lithology is made up of three minerals, then the Mlith and Nlith values can be linearly triangulated to find the fraction of the minerals.
      12: D = (Mlith * (NLITH2 - NLITH1) + Nlith * (MLITH1 - MLITH2)
               + MLITH2 * NLITH1 - MLITH1 * NLITH2) / (MLITH1 * (NLITH3 - NLITH2)
               + MLITH2 * (NLITH1 - NLITH3) + MLITH3 * (NLITH2 - NLITH1))
      13: E = (D * (NLITH3 - NLITH1) - Nlith + NLITH1) / (NLITH1 - NLITH2)
      14: Vmin1 = MAX(0, 1 - D - E) / (MAX(0, 1 - D - E) + MAX(0, D) + MAX(0, E))
      15: Vmin2 = MAX(0, E) / (MAX(0, 1 - D - E) + MAX(0, D) + MAX(0, E))
      16: Vmin3 = (1.00 - Vmin1 - Vmin2)

Where:
  DTC = sonic log reading (usec/ft)
  DTCc = sonic log reading corrected for shale (usec/ft)
  DTCSH = sonic log reading in 100% shale (usec/ft)
  DELTW = sonic log reading in 100% water (usec/ft)
  DENS = density log reading (gm/cc)
  DENSc = density log reading corrected for shale (gm/cc)
  DENSW = fluid density (gm/cc)
  Mlith = sonic density lithology factor (fractional)
  MLITH1 = Mlith of first mineral (fractional)
  MLITH2 = Mlith of second mineral (fractional)
  MLITH3 = Mlith of third mineral (fractional)
  Nlith = neutron density lithology factor (fractional)
  NLITH1 = Nlith of first mineral (fractional)
  NLITH2 = Nlith of second mineral (fractional)
  NLITH3 = Nlith of third mineral (fractional)
  PHIdc = density porosity corrected for shale (fractional)
  PHIDSH = density log reading in 100% shale (fractional)|
  PHIN = neutron log reading (fractional)|
  PHInc = neutron log porosity corrected for shale (fractional)
  PHINSH = neutron log reading in 100% shale (fractional)
  PHIsc = sonic log porosity corrected for shale (fractional)
  Vsh = volume of shale (fractional)
  Vmin1 = relative volume of first mineral (fractional)
  Vmin2 = relative volume of second mineral (fractional)
  Vmin3 = relative volume of third mineral (fractional)
 

COMMENTS:
NOTE: all log data must be converted to English Units before use - usec/m * 0.3048 = usec/ft and kg/m3 * 0.001 = g/cc.

All Vmin results must be multiplied by Vrock to get true mineral volumes (V1, V2, V3) from relative mineral volumes. Vrock = 1.00 - PHIe - Vsh.

By comparing computed values of Mlith and Nlith with those in the table below, or by plotting them on an Mlith - Nlith crossplot, rock matrix can usually be identified. The method is relatively independent of porosity, except for dolomite.

These two variables are usually called M and N, but they can be confused with the cementation exponent M and the saturation exponent N, so we have changed their names to reduce confusion.

The end points for the common minerals are plotted below.

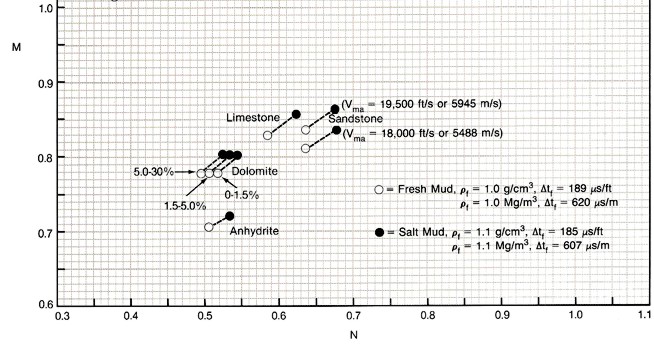
Mlith vs Nlith crossplot for two or three mineral models

NUMERICAL EXAMPLE:
1. Assume data from 2135 - 2153 meters in Classic Example 2.
PHID = 0.015
PHIN = 0.15
DTCc = DTC = 190 usec/m = 61 usec/ft
DENSW = 1000 kg/m3 = 1.00 gm/cc
DENSMA = 2710 kg/m3 = 2.71 gm/cc
Vsh = 0.0
DENSc = 0.015 * 1.00 + (1 - 0.015) * 2.71 = 2.684
Nlith = (1.00 - 0.15) / (2.684 - 1.00) = 0.50
Mlith = 0.01 * (188 - 61) / (2.684 - 1.00) = 0.77

The closest values in the table represent dolomite (Mlith = 0.778 and Nlith = 0.516), so this interval is very likely dolomite.

Lithology from Alith-Klith Methods
The Alith-Klith method, like the Mlith-Nlith method, is used to identify matrix lithology. The term A can be confused with the tortuosity exponent A used in the water saturation equation, hence we use the term Alith and Klith instead of A and K.

The input data to these algorithms must be shale corrected, must be in limestone porosity units and must be in English units before processing begins.

Shale correct raw data:
      21: PHIdc = PHID - Vsh * PHIDSH
      22: PHInc = PHIN - Vsh * PHINSH
      23: PHIsc = (DELT - (1 - Vsh) * 47.3 - Vsh * DELTSH) / (188 - 47.3)
      24: DENSc = PHIdc + (1 - PHIdc) * 2.71
      25: DTCc = PHIsc * 188 + (1 - PHIsc) * 47.3

Calculate Alith and Klith:
      26: Alith = (DENSc - DENSW) / (1.00 - PHInc)
      27: Klith = 0.01 * (DTCW - DTCc) / (1.00 - PHInc)

2-Mineral Model Using Alith
If the usual lithology is made up of two minerals, then the Alith and Klith values can each be linearly interpolated to find the fraction of the minerals.
      28: Vmin1 = (Alith - ALITH2) / (ALITH1 -AMLITH2)
      29: Vmin2 = 1.00 - Vmin1


2-Mineral Model Using Klith
      30: Vmin1 = (Klith - KLITH2) / (KLITH1 - KLITH2)
      31: Vmin2 = 1.00 - Vmin1

3-Mineral Model Using Alith and Klith
If the usual lithology is made up of three minerals, then the Alith and Klith values can be linearly triangulated to find the fraction of the minerals.
      32: D = (Alith * (KLITH2 - KLITH1) + Klith * (KLITH1 - ALITH2)
               + ALITH2 * KLITH1 - ALITH1 * KLITH2) / (ALITH1 * (KLITH3 - KLITH2)
               + ALITH2 * (KLITH1 - KLITH3) + ALITH3 * (KLITH2 - KLITH1))
      33: E = (D * (KLITH3 - KLITH1) - Klith + KLITH1) / (KLITH1 - KLITH2)
      34: Vmin1 = MAX(0, 1 - D - E) / (MAX(0, 1 - D - E) + MAX(0, D) + MAX(0, E))
      35: Vmin2 = MAX(0, E) / (MAX(0, 1 - D - E) + MAX(0, D) + MAX(0, E))
      36: Vmin3 = (1.00 - Vmin1 - Vmin2)

Where:
  Alith = density neutron lithology factor (fractional)
  DTC = sonic log reading (usec/ft or usec/m)
  DTCc = sonic log reading corrected for shale (usec/ft or usec/m)
  DTCSH = sonic log reading in 100% shale (usec/ft or usec/m)
  DTCW = sonic log reading in 100% water (usec/ft or usec/m)
  DENS = density log reading (gm/cc or kg/m3)
  DENSc = density log reading corrected for shale (gm/cc or kg/m3)
  DENSW = fluid density (gm/cc or kg/m3)
  Klith = sonic neutron lithology factor (fractional)
  PHIdc = density porosity corrected for shale (fractional)
  PHIDSH = density log reading in 100% shale (fractional)
  PHIN = neutron log reading (fractional)
  PHInc = neutron log porosity corrected for shale (fractional)
  PHINSH = neutron log reading in 100% shale (fractional)
  PHIsc = sonic log porosity corrected for shale (fractional)
  Vsh = volume of shale (fractional)

COMMENTS:
Note that Alith is the inverse of Nlith and that Klith is the ratio Mlith/Nlith. The data for common minerals is plotted below.

To calculate 2 or 3 mineral models, use the same math as the Mlith-Nlith Section, but replace Mlith with Alith and Nlith with Klith.

NUMERICAL EXAMPLE:
1. Assume the same data as before:
PHID = 0.015
PHIN = 0.15
DELT = 190 usec/m = 61 usec/ft
DENSc = 0.015 + (1.0 - 0.015) * 2.71 = 2.684
Klith = 0.01 * (188 - 61) / (1 - 0.15) = 1.52
Alith = (2.684 - 1.00) / (1 - 0.15) = 1.98

Again, these values are close to the dolomite point, so the rock is assumed to be dolomite.

Lithology from Mlith-Plith Method
An alternate version of this model can be made by replacing Nlith with Plith = PE / (DENS - DENSW) - density in gm/cc. This avoids the use of the neutron log in cases where it has little lithology discrimination, such as in igneous rocks.

Shale correct all data:
 

      1: PHIdc = PHID - Vsh * PHIDSH
      2: PEc = PE - Vsh * PESH
      3: PHIsc = (DTC - (1 - Vsh) * 47.3 - Vsh * DTCSH) / (188 - 47.3)
      4: DENSc = PHIdc + (1 - PHIdc) * 2.71
      5: DTCc = PHIsc * 188 + (1 - PHIsc) * 47.3

Calculate Mlith and Plith
      6: Plith =  PEc / (DENSc - DENSW)
      7: Mlith = 0.01 * (DTCW - DTCc) / (DENSc - DENSW)

2-Mineral Model Using Mlith
If the usual lithology is made up of two minerals, then the Mlith and Nlith values can each be linearly interpolated to find the fraction of the minerals.
      8: Vmin1 = (Mlith - MLITH2) / (MLITH1 - MLITH2)
      9: Vmin2 = 1.00 - Vmin1

2-Mineral Model Using Plith
      10: Vmin1 = (Plith - PLITH2) / (PLITH1 - PLITH2)
      11: Vmin2 = 1.00 - Vmin1

3-Mineral Model Using Mlith and Plith
If the usual lithology is made up of three minerals, then the Mlith and Plith values can be linearly triangulated to find the fraction of the minerals.
      12: D = (Mlith * (PLITH2 - PLITH1) + Plith * (MLITH1 - MLITH2)
               + MLITH2 * PLITH1 - MLITH1 * PLITH2) / (MLITH1 * (PLITH3 - PLITH2)
               + MLITH2 * (PLITH1 - PLITH3) + MLITH3 * (PLITH2 - PLITH1))
      13: E = (D * (PLITH3 - PLITH1) - Plith + PLITH1) / (PLITH1 - PLITH2)
      14: Vmin1 = MAX(0, 1 - D - E) / (MAX(0, 1 - D - E) + MAX(0, D) + MAX(0, E))
      15: Vmin2 = MAX(0, E) / (MAX(0, 1 - D - E) + MAX(0, D) + MAX(0, E))
      16: Vmin3 = (1.00 - Vmin1 - Vmin2)

Where:
  DTC = sonic log reading (usec/ft)
  DTCc = sonic log reading corrected for shale (usec/ft)
  DTCSH = sonic log reading in 100% shale (usec/ft)
  DTCW = sonic log reading in 100% water (usec/ft)
  DENS = density log reading (gm/cc)
  DENSc = density log reading corrected for shale (gm/cc)
  DENSW = fluid density (gm/cc)
  Mlith = sonic density lithology factor (fractional)
  Plith = PE density lithology factor (fractional)
  PHIdc = density porosity corrected for shale (fractional)
  PHIDSH = density log reading in 100% shale (fractional)|
  PE = photo electric log reading (fractional)|
  PEc = photo electric log corrected for shale (fractional)
  PESH = photo electric log  reading in 100% shale (fractional)
  PHIsc = sonic log porosity corrected for shale (fractional)
  Vsh = volume of shale (fractional)

COMMENTS:
This model is very effective in granite reservoirs.

To calculate 2 or 3 mineral models, use the same math as the Mlith-Nlith Section, but replace Nlith with Plith.

MATRIX ROCK PARAMETERS
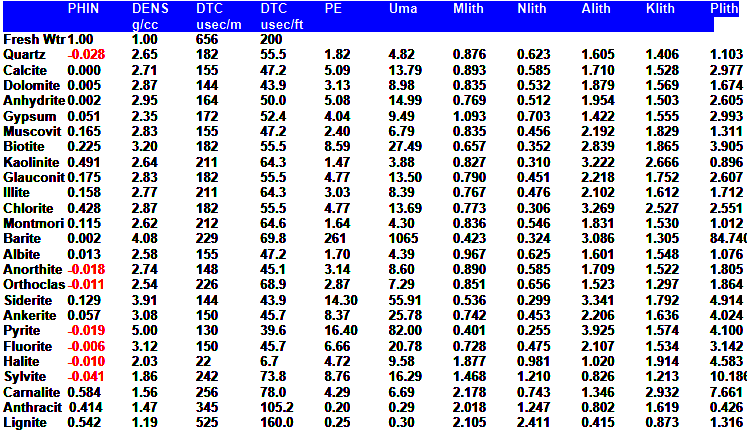