POTASH basicS
Potash refers to potassium compounds and potassium-bearing minerals, the most common being potassium chloride. The distinguishing characteristic of potash minerals on well logs is their relatively high radioactivity, due to the potassium-40 isorope, and their relatively low density compared to other common sedimentary rocks.

The term "potash" comes from the old method of making potassium carbonate  by leaching wood ashes and evaporating the solution in large iron pots, leaving a white residue called "pot ash".

Later, "potash" became the term widely applied to naturally occurring potassium salts and the commercial product derived from them. The main potash salts are sylvite, Carnallite, langbeinite, and polyhalite, mixed in varying concentrations with halite (rock salt). The main use of potash is as fertilizer.
 

Sylvinite is the most important ore for the production of potash in North America. It is a mechanical mixture of sylvite (KCl, or potassium chloride) and halite (NaCl, or sodium chloride). Most Canadian operations mine sylvinite with proportions of about 31% KCl and 66% NaCl with the balance being insoluble clays, anhydrite, and in some locations carnallite.

Sylvinite ores are beneficiated by flotation, dissolution,-recrystallization, "heavies" separations, or combinations of these processes.

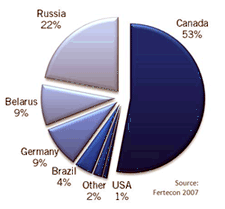The major source of potash in the world is from the Devonian Prairie Evaporite Formation in Saskatchewan, which provides 11 million tons per year. Russia is second at 6.9 million and the USA (mostly from New Mexico) at 1.2 million tons per year. A dozen other countries in Europe, Middle East, and South America produce potash from evaporite deposits.

Potash can be mined mechanically by underground machinery or by solution mining using ambient or warmed water. Halite (salt) for human  use or road de-icing can be mined the same ways. Potash ores contain halite as well, so the by-product of potash extraction is road salt. In earlier times, salt was more valuable per ounce than gold, as it was essential to human life. A person "worth his salt" was one who contributed his fair share to the community.



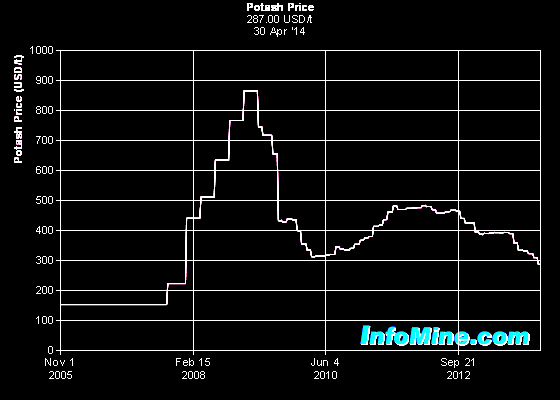Potash prices have undergone a flurry of variation since 2005, after many years of relatively stable values. A perceived shortage of supply moved the price from around $200 per tonne to nearly $900 per tonne, falling quickly to the $300 to $500 range. The breakup of the Russian / Belerus potash cartel in 2012 pushed prices into the $300 per tonne range and by 2014 appeared to be stabilized near this value. The future is unpredictable.









 

PROPERTIES OF POTASH Minerals
Potassium is radioactive so the gamma ray log is used to identify potash bearing zones. Potash minerals have distinctive physical properties on other logs, so conventional multi-mineral models can be used to determine the mineral mixture, just as we do in carbonates in the oil and gas environment.

For consistency, potash ore and fertilizer concentrations are rated by their equivalent K2O content. Some literature can be confusing because they rate the ore by its potassium content (K) or potassium chloride content (KCl), The table below lists the physical properties of potash minerals, including K and K2O values. The GR (API units) entry in the table do not seem to match any known correlation, so some caution is urged.

The GR values shown above will vary with tool type and calibration is performed only at low GR flux (about 200 - 250 API units). Quoted values for sylvite are >500, 753, 953, 1046. A correlation between sylvite or K2O content should be done to calibrate a particular tool type whenever possible. GR values for the other minerals can be prorated based on their K or K2O content.
 

Actual sonic travel time in halite and sylvite may be slightly higher than shown above due to occluded water. The Vp/Vs ratio for most salts is close to 1.9 so shear travel time is close to 1.9 times compressional travel time.

The above physical properties are used in the standard 2- and 3-mineral models, simultaneous equation models, and multi-mineral probabilistic models. Choose the mineral mix to match the actual mineralogy as described in cores or samples. Add clay or quartz to account for insolubles and occluded water if enough independent log curves are available.

 

REFERENCES:
   1. Quantitative Log Evaluation of the Prairie Evaporite Formation of Saskatchewan
   E. R. Crain, P.Eng., W.B. Anderson, P.Eng.
   Journal of Canadian Petroleum Technology, Quebec City and Edmonton, Jul-  Sep, 1966
   As published, 1966
   As written with legible illustrations, 1964
   Program for IBM 1620, 1964

   2. Defining Evaporite Deposits with Electrical Well Logs
   R. P. Alger, E. R. Crain, P.Eng.
   Trans Northern Ohio Geological Society - Second Symposium on Salt, Cleveland, 1966
  

   3. Potash Redux
   E. R. Crain, P.Eng., CWLS InSite, Dec 2010
  
 

LOGGING IN POTASH WELLS

The minimum logging program for a potash interval is gamma ray and a neutrom log. A sonic, density, and PE logs are useful in assessing accessory minerals. A resistivity log is usually required elsewhere in the rest of the wellbore so it is usually run in combinatation with the others. Here are some examples.

Example  of a 1964 gamma ray neutron log from Saskatchewan. Note the primary GR with 2 backup curves in Track 1. This is hard to use quantitatively, so an alternative GR dis]lay was common before the digital era, as shown below.

.
Example  of a 1964 3-track gamma ray log presentation, common before the digital era. GR scale is 0 to 600 API units. Log data values picked from these logs are used to create a transform relating the log data to core assay data. An example of such a transform is shown later on this webpage.


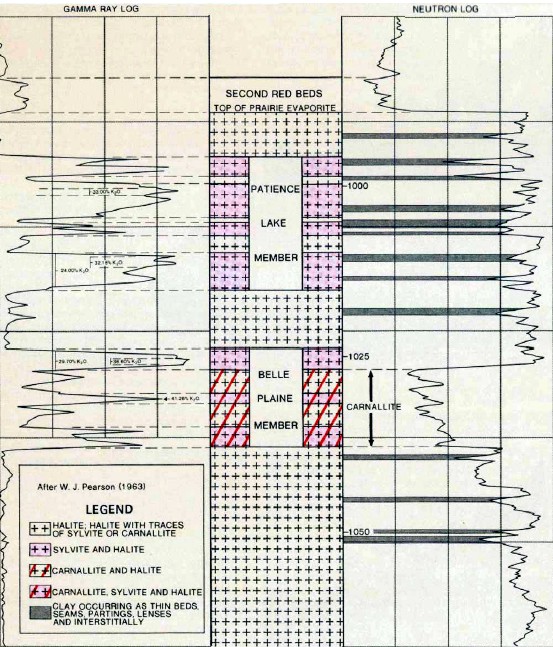
Example gamma ray and neutron log from Saskatchewan showing halite, sylvite, Carnallite, and clay responses. In the exploration heyday in Saskatchewan in the 1960's, we presented the gamma ray across 3 tracks of the log, giving a scale of 0 to 450 or 0 to 600 API units across 7.5 inches of paper. This was sufficient resolution for accurate evaluation and eliminated the need for GR backup curves cramped into Track 1.
 

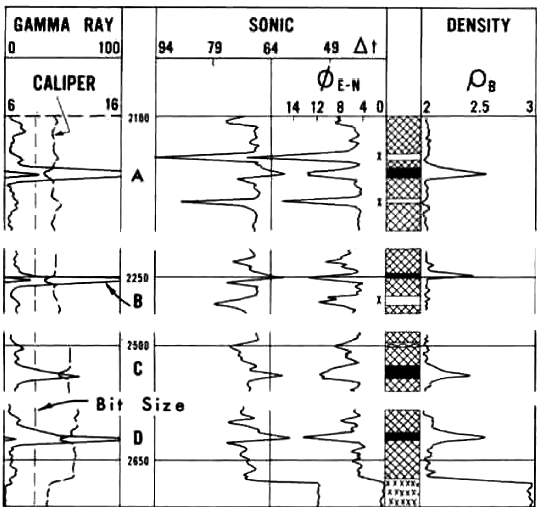
1970's era logs in a potash interval in New Mexico. Visual analysis is based on review of the four log
 curves: GR, sonic, neutron, and density.
 

POTASH MINERAL IDENTIFICATION FROM CROSSPLOTS
Crossplots of well log data have been used for many years in the oil, gas, and sedimentary mineral industries. A number are shown below -- they are not found in standard service company chartbooks.

The most useful is a crossplot of gamma ray versus neutron porosity. Commercial potash ores are anhydrous (no water of hydration), such as sylvite and langbeinite, so the neutron log reads near zero. Hydrated potash minerals will have non-zero neutron response, such as Carnallite, polyhalite, and kainite. High gamma ray response distinguishes all these minerals from other zero porosity minerals, such as halite and anhydrite, and from porous minerals, such as calcite, dolomite and clay.

Potash beds seldom contain pure minerals; usually they are made of a mixture of one or more potash minerals with halite. Thus data points will fall on trend lines joining the pure mineral points. The best examples are the Potash Identification Plots (PID plots) contained in "Simple Screening Technique for Identifying Commercial Potash", by Donald G. Hill Ph.D., AAPG, 2019. Here are some examplws.

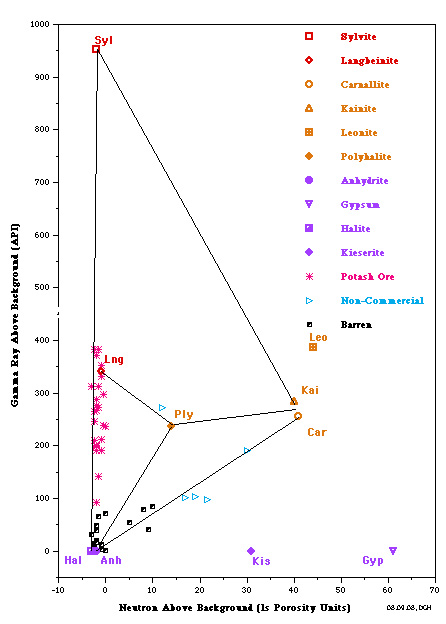
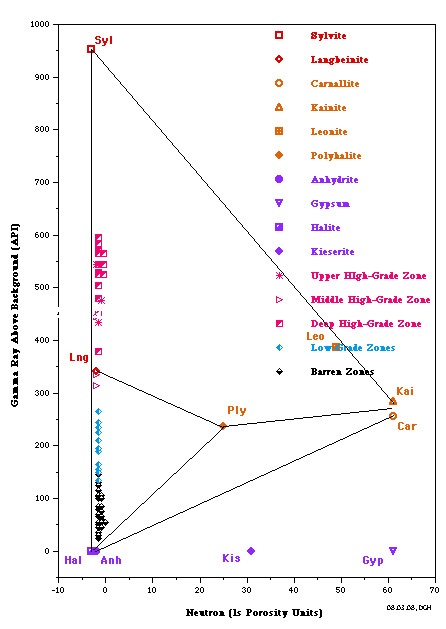
PID Plots for Prairie Evaporite in Saskatchewan (left) and Windsor Salt jn Nova Scotia (right). Both show data points along the near vertical Sylvite - Langbeinite - Halite trend line, indicating commercial grade potash ore. Only the Saskatchewan example shows some data trending toward the non-commercial Carnallite data point. Note that the GR scale on the vertical axis is for a moden logging tool with a linerar response. For older tools, the Y-axis could be replaced with a K2O axis, derived from the original Crain non-linerar relationship.


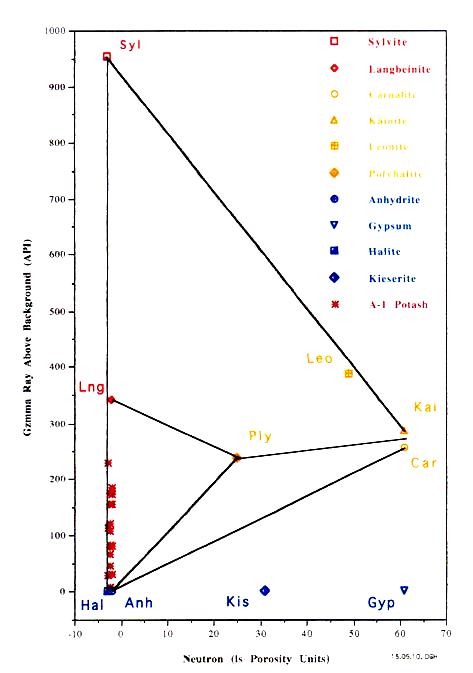
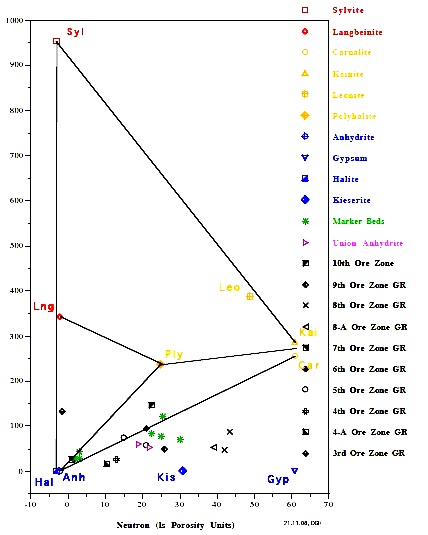
The Michigan Basin example (left) shows only commercial grade potash ore in this well. The New Mexico example (right) shows only non-commercial ore in this well.
 

The following crossplot illustrations were derived from the well logging literature.
 

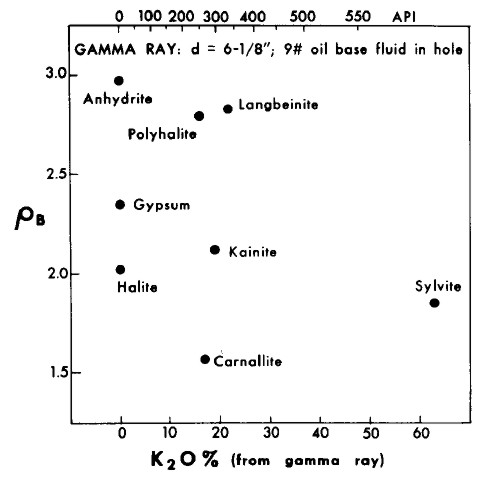
Gamma ray and K2O content versus density crossplot of evaporite minerals used for mineral identification. Note that the GR scale is non-linear based on Crain's correlation of 1960's era logs; modern GR logs are linear beyond 1000 API units and require a different calibration to K2O content. 


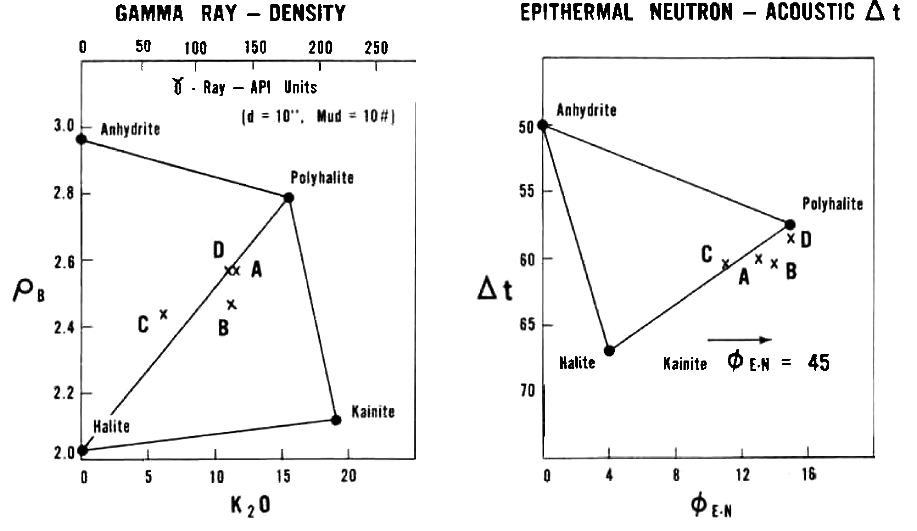
Density versus K2O fs and Sonic versus Neutron Crossplots for some potash minerals.


 

POTASH ANALYSIS - OLDER LOGS

Since potassium is radioactive, the K2O content can be derived from gamma ray logs, and this technique has been used since the 1960's. In 1964, I was stationed in Lanigan, Saskatchewan to run logs in potash exploration wells. While there, I scrounged a personal tour of the Esterhazy potash mine, then only two years old. This was the first and only time I have seen geological structure and stratigraphy from the "inside" of the rock. Truly amazing!

No direct calibration between GR and K2O had been developed up to that time, so I convinced a client to let me see his core assay data. After adjusting for hole size, mud weight, and bed thickness, a reasonable relationship was found, and was published as "Quantitative Log Evaluation of the Prairie Evaporite Formation of Saskatchewan" by E. R. Crain and W. B. Anderson, Journal of Canadian Petroleum Technology, July--September, 1966.

The work was subsequently reprinted in five other papers by various authors, some included updates as tool technology evolved. The original GR correlation was unchanged, widely distributed, and was the standard for potash analysis from oilfield style logs run prior to the era of digital logs in the 1980's. Most analog oil field GR logs were non-linear above about 300 API units due to dead time in the counting circuit. These older logs are still available in the well files and were recently used by Saskatchewan Industry and Resources to update their potash isopach and ore grade maps.

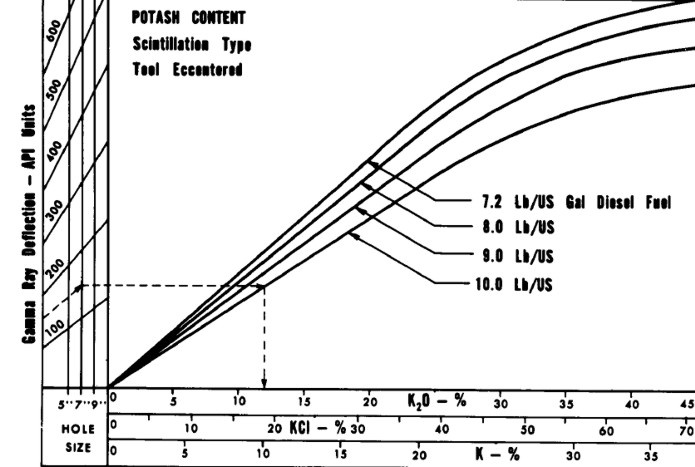
K2O versus Gamma Ray relationship for analog Schlumberger tools circa 1960 - 1975, run in open hole with oil based mud. Tools from other service companies may differ. Correlation between log and core assay data for specific cases is strongly recommended. Modern gamma ray logs respond in a more linear fashion and slope may be different due to more efficient detectors.

GAMMA RAY BOREHOLE CORRECTIONS
The hole size and mud weight corrections derived from the data, and embedded in the above chart, were:
      1. GRh = GR * (1.0 +.0.05 * (HS - 6.0)) + (320 * (HS - 6.0)) / (GR + 100.0)
      2. GRc = GRh * (1.0 + 0.10 * (WM - 7.2))

Where:
  GR = gamma ray log reading (API)
  GRc = GR corrected for hole size and mud weight (API)
  GRh = GR corrected for hole size (API)
  HS = hole size (inches)

  WM = mud weight (lb/gal)

POTASH ORE GRADE FROM GAMMA RAY
K2O content was derived from GRc using the lookup table shown at the right. It is linear up to 400 API units and exponential thereafter. Values in the table represent a 6 inch borehole filled with diesel at 7.2 lb/gal. The linear portion of the lookup table is represented by:
      3: IF GRc <= 400
      4: THEN K2O = 0.05625 * GRc
      5: OTHERWISE Use Lookup Table

The slope in the above equation can be determined by correlation to core assay data for other hole sizes or other tool types.

The non-linear relationship must be honoured while analyzing these older logs for potash. The effect is negligible for conventional oil field applications. Modern digital tools are linear up to about 1000 API units so the discussion in this Section does not apply.

A 1967 paper showed a linear GR relationship up to 650 API units for the McCullough tool, but its use was not widespread in Canada. That graph showed 600 API units was equivalent to 45% K2O, identical to my original data, but the slope of the line at lower GR readings was different. No mud weight correction was implied but a bed thickness correction similar to mine was presented.

In the analog era, GR logs were calibrated to a secondary standard based on the API GR test pit in Houston which contained an artificial radioactive formation defined as 200 API units in an 8 inch borehole filled with 10 lb/gal mud.

However, there were no published borehole size or mud weight correction charts for the GR log. These effects are large enough to seriously compromise the correlation.

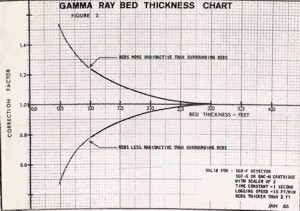
BED THICKNESS ISSUES
Bed thickness corrections are also needed for beds less than 3 feet thick (1 meter). This is true even for modern logs. The chart shown at the right illustrates the importance of normalizing the GR log for these factors. Unfortunately, my original data plots for this work were lost in the bowels of a Schlumberger shredder many years ago - it would have been nice to recalibrate the work with the power of non-linear regression in a good statistics package.

NON-OILFIELD GAMMA RAY TOOLS
Many potash exploration wells in the USA and elsewhere were logged with slim hole GR tools intended for uranium work. While they may have been more linear, they were not usually calibrated to any standard, suffered from larger borehole effects, and were recorded in counts per second (cps). Specific correlations to core assay data on a well by well basis are required for these wells.

USING ANCIENT NEUTRON LOGS
Due to the water of hydration associated with Carnallite, the neutron log is very useful for distinguishing between Carnallite and sylvite. High neutron count rates mean low hydrogen index, thus sylvite and not Carnallite.

To quantify the relative amounts of Carnallite and sylvite, the neutron response must be converted to porosity from count rates using the standard semi-logarithmic relationship. A typical transform for a 1960's era Schlumberger tool is shown at the left. Charts for other tools can be found in ancient service company chart books.

With the advent of the sidewall neutron log in 1969 and later the compensated neutron log, this transform was no longer required.

USING SONIC AND DENSITY LOGS
Some wells were logged with sonic and/or density logs in addition to the neutron log, which also could be used quantitatively with the GR and neutron to provide a potash assay based on logs. This was important where core was lost or for regional exploration when core data, but not the logs, were proprietary. The logic behind these models is shown below. A later Section of this article deals with the use of more modern logs.

POTASH  ModelS - OLDER LOGS
My original computer program for potash analysis was written for the IBM 1620 in Regina in 1964. The model was based on four simultaneous equations that define the response of the available logs. Although this seems like a long time ago, nothing has changed except the improved tool accuracy. If you want to analyze the older log suites, here's how to do it.

The minerals sought are halite (rock salt), sylvite, Carnallite, and insolubles or clay. The only logs available on old wells are resistivity, sonic, neutron, and total gamma ray. The resistivity is not a helpful discriminator, except as a shale bed indicator, so it is not used in the simultaneous solution. These evaporite beds contain potassium and ore grade is measured in units of potassium oxide (K2O). K20 is obtained from a gamma ray log, corrected for borehole size and mud weight, using a non-linear transform derived from core assay data. In middle aged wells, the density log is also helpful, and in modern wells the PE curve can be added. Further, the gamma ray response is linear on modern wells so the transform to K2O is not as difficult to obtain.

The equations are:
      1.00 = Vsalt + Vsylv + Vcarn + Vclay
      K20 = 0.00 * Vsalt + 0.63 * Vsylv + 0.17 * Vcarn + 0.05 * Vclay
      PHIN = 0.00 * Vsalt + 0.00 * Vsylv + 0.65 * Vcarn + 0.30 * Vclay
      DTC = 67 * Vsalt + 74 * Vsylv + 78 * Vcarn + 120 * Vclay

K2O is obtained, after borehole correcting the GR, from the equations and lookup table shown earlier, or from a fresh correlation based on specific data from the wells under study. Note that the chart and table given earlier are in percent K2O and this set of equations expects fractional units for K2O, neutron porosity, and all output volumes. Parameters in the sonic equation are in usec/ft.

When solved by algebraic means, these equations become:
      1: Vclay = 0.0207 * DTC - 0.23 * K20 - 0.29 * PHIN - 1.3891
      2: Vcarn = 1.54 * PHIN - 0.46 * Vclay
      3: Vsylv = 1.59 * K20 - 0.41 * PHIN + 0.04 * Vclay
      4: Vsalt =  1.00 - Vclay - Vsylv - Vcarn

These equations were derived with DELT in usec/ft. All constants will be different if DELT is in us/m.

To convert from mineral fraction to K2O equivalent (K2O equivalent is the way potash ores are rated), the final analysis follows:
      5: K2Osylv = 0.63 * Vsylv
      6: K2Ocarn = 0.17 * Vcarn
      7: K2Ototal = K2Osylv + K2Ocarn

EFFECT OF OCCLUDED WATER
If occluded water (V) is added to the desired results, the equations become:
      1.00 = Vwtr + Vsalt + Vsylv + Vcarn + Vclay

Where Vwtr = PHIN value in pure salt above the zone of interest.

The occluded water has zero gamma ray emission so the second equation remains unchanged:
      K20 = 0.00 * Vsalt + 0.63 * Vsylv + 0.17 * Vcarn + 0.05 * Vclay

The porosity is read directly by the neutron log, hence, the third equation becomes:
      PHIN = 1.00 * Vwtr + 0.00 * Vsalt + 0.00 * Vsylv + 0.65 * Vcarn + 0.30 * Vclay

The sonic equation becomes:
      DELT = C + 67 * Vsalt + 74 * Vsylv + 78 * Vcarn + 120 * Vclay

Where C = DELT in salt minus 67 usec/ft.

Reduction of these equations results in:
      8:   Vclay = 0.0207 * (DELT - C) - 2.23 * K20 - 0.29 * (PHIN - V) - 1.3891
      9:   Vcarn = 1.54 * (PHIN - V) - 0.64 * Vclay
      10: Vsylv = 1.59 * K20 - 0.41 * (PHIN - V) - 0.04 * Vclay
      11: Vsalt = 1.00 - Vsylv - Vcarn - Vclay - Vwtr

Conversion to K20 equivalent remains the same as before. Note that mineral fractions are in volume fractions. To convert to weight fraction, one more step is needed. By using the density of each mineral times the volume fraction, summing these to get the total rock weight, then dividing each individual weight by the rock weight, we get weight fraction of each. This allows comparison to core assay data which are reported in weight fraction or percent. The same math is used in tar sands and coal analysis to allow comparison to lab data.

      12: WTclay = Vclay * 2.35
      13: WTcarn = Vcarn * 1.61
      14: WTsylv = Vsylv * 1.98
      15: WTsalt = Vsalt * 2.16 
      16: WTwtr  = Vwtr * 1.10
      17: WTrock = WTclay + WTcarn + WTsylv + WTsalt + WTwtr

Note that the densities in the above equations are the true density values, not the electron densities used in the original simultaneous equations.

Mass fraction or weight percent values are obtained b dividing individual weights by WTrock. foer example:
      18: Wsylv = WTsylv / WTrock
      19: Wcarn = WTcarn / WTrock
      20: WT%sylv = 100 * Wsylv
      21: WT%carn = 100 * Wcarn

Where:
  Vxxx = volume fraction of a component
  WTxxx = weight of a component (grams)
  Wxxx = mass fraction of a component
  WT%xxx = weight percent of a component

COMMENTS
These equations show the use of constraints (Vwtr and C) on the otherwise linear simultaneous equations. The first set of equations is exactly determined, and the second set are underdetermined until Vwtr and C are defined.

If the density or PE equation were added, then the set would be exactly determined and the strategy of finding Vwtr and C in the pure salt bed would not be needed. This work was done in Saskatchewan before density logs were common, so the density equation was not used at that time.

POTASH MODELS - MODERN LOGS

With a modern suite of calibrated logs, we can use conventional multi-mineral models to calculate a potash assay. With GR, neutron, sonic, density, and PE, we can solve for halite, sylvite, Carnallite, clay (insolubles or shale stringers), and water (occluded in many salts as isolated pores). The potassium curve from a spectral gamma ray log might also prove useful, if the detector system is linear and does not saturate. Alternate mineral models are quite possible in other potash areas of the world.

The mathematical methods are covered in the Lithology Chapters elsewhere in this Handbook. Matrix rock properties for the minerals were shown earlier in this article. Water is treated as a "mineral" so that it can be segregated from the water of hydration in Carnallite.

Probabilistic analysis methods are also used with modern log suites. Here, the mineral mixture can be underdetermined, allowing the program to find the best mix at any particular depth point.

The first step is to correct the gamma ray for borehole and mud weight effects, using the appropriate service company correction charts. The other logs seldom need much correction as the potash is not deep or hot. However, if a water based mud was used, it will have a high salinity, so a salinity correction for the neutron log may be required.

The second step is to confirm the GR to K2O correlation using any available potash core assay data. Since modern GR logs are more linear than older tools, the relationship should be a relatively straight line and can be extended beyond the available core data, as shown at the right.

SPECIAL CASES
There are numerous situations which require special treatment. These include:

  1. an incomplete open hole logging suite

  2. logs run through casing

  3. logs run with GR in counts per second

  4. logs run where thin beds predominate

  5. combinations of the above.

Incomplete Logging Suite

Here we must include fewer minerals in the model. Isolated water is easy to ignore, and insoluble clay comes next, although it is an important economic factor in the extraction process. In the worst case, we might need to settle for K2O from the gamma ray and a sylvite / Carnallite discriminator based on the neutron log. This situation occurs most often when potash geologists are using logs in wells drilled originally for oil or gas, in which potash evaluation was not considered as a priority.

Through Casing Logs

The most obvious problem will be to correct the gamma ray log for casing size and weight, cement sheath thickness, and borehole fluid weight using service company correction charts. Where core assay data is available from the well or from reasonably close offsets, the GR to K2O relationship can be confirmed. The second problem is usually an incomplete logging suite, as described above. If a through casing neutron log is available, scaled or not, a Carnallite flag can be created.

GR in Counts per Second
Many potash wells are drilled as stratigraphic test wells and are not intended to be completed. They are often drilled as slim holes and slim hole GR logs must be run. Some of these logs may be calibrated to the API GR standard; many are not. In any case the GR to K2O correlation must be established for each tool type and adjusted if mud weight or borehole size varies between wells. Bear in mind that the core retrieved from a slim hole is volumetrically much smaller than full size cores. Variations between log and core data is expected to be somewhat larger in slim holes.

Thin Bed Problems
This issue affects all logs used for all purposes, but can seriously affect potash evaluation in areas where thin beds predominate. An approach was shown earlier using a bed thickness correction chart. Another approach is to correlate K2O times thickness to GR times thickness instead of a direct GR to K2O transform. This is best suited to hand picked data, as thickness is not so easily determined automatically in most log analysis software. The US Geological Survey published an example, originally developed by Jim Lewis of Intrepid Mining for a New Mexico case study. The pertinent crossplots from his work are shown below. The regression has much less scatter on the GR times thickness plots. This method was originally suggested in a 1967 paper describing the use of McCullough GR logs for potash evaluation.

 
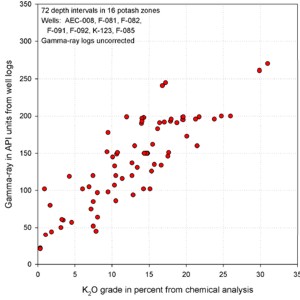
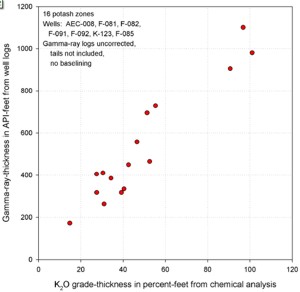
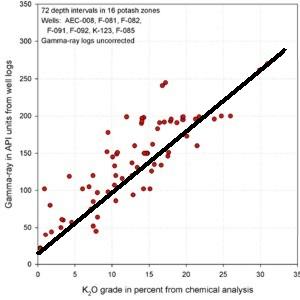
GR in API units vs K20 (left) shows poor correlation due to thin bed effects. GR-thickness vs K2O-thickness products (right) correlate much better (regression lines not shown).

 
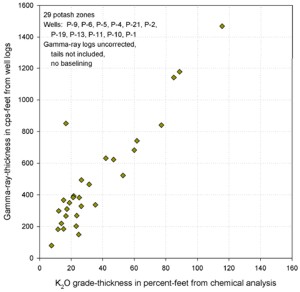
Similar graphs for some USGS GR data in cps show that the GR-thickness product is a better predictor of potash content than GR by itself in thinly bedded potash zones..

Combinations of the Above
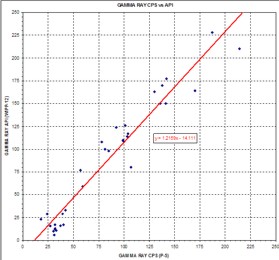It would be unusual if there were no problems to solve. Logs run in different areas by a variety of service companies need to be normalized to some single standard. Borehole and casing effects need to be handled first. Then normalizing oilfield and strat hole gamma ray logs can be done by correlating potash beds between near offset wells. It would be nice if both wells also had core assay data but this is seldom the case. At right is a comparison of USGS log picks over 29 potash intervals showing the regression against the API units for the same zones in the nearest oilfield well. The equation of the line can be used to convert all USGS logs to API units in this particular project area.

Ancient GR logs could be rescaled with a non-linear transform to make them respond similarly to modern logs. Once the conversion is made, computer analysis is easier and cross sections look better.


POTASH ANALYSIS EXAMPLES - OLDER LOGS
A sample of computed results from this log analysis model compared to core data is shown below. The GR was borehole corrected but no bed thickness corrections were applied.

Example log analysis showing excellent match to core data (circa 1964). Raw data is shown but note the scales are opposite polarity to normal.


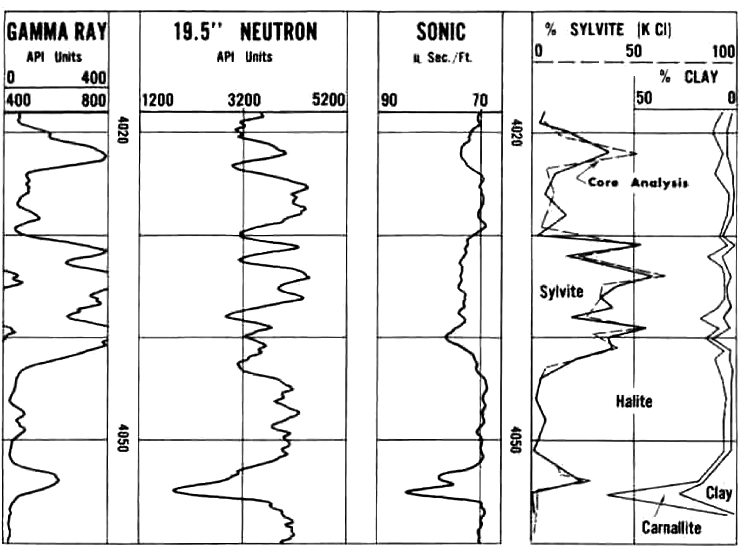
Another Saskatchewan example with sylvite, salt, and clay compared to core assay, grading to Carnallite near the base, normal log presentations.

Potash evaluation of 1960's logs with a modern log analysis program. The core gamma ray (dashed curve, Track 1) reads considerably higher than the open hole GR log (solid curve). Using Crain's original non-linear algorithms on the log data, results match core assay data (see data in K2OS and K2OC tracks). A linear transform would be needed to calibrate K2O from the core gamma curve.
 

POTASH ANALYSIS EXAMPLES - OLDER LOGS

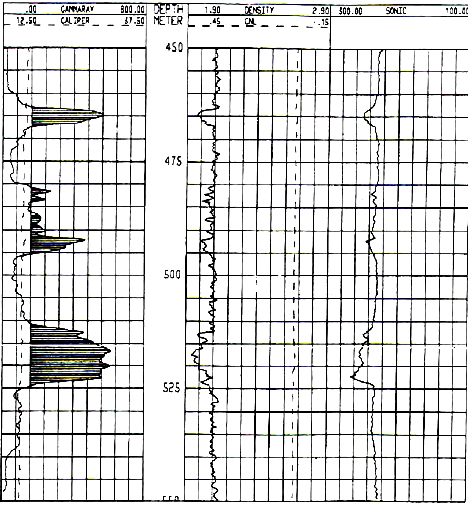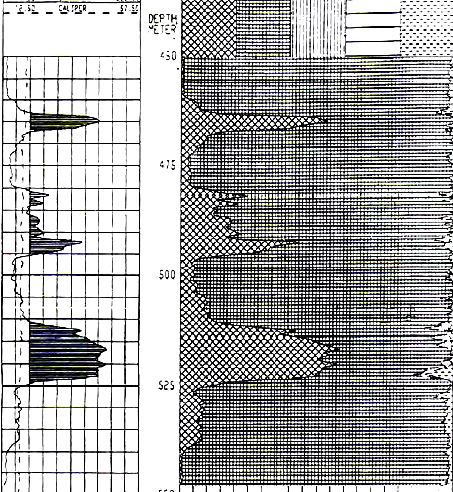
1990's example from the Windsor Salt formation in Nova Scotia. Note GR scale is 0 to 800 API units, shaded when curve is greater than 160 API units. Image courtesy of Don Hill, JAG Vol 30, 1993.

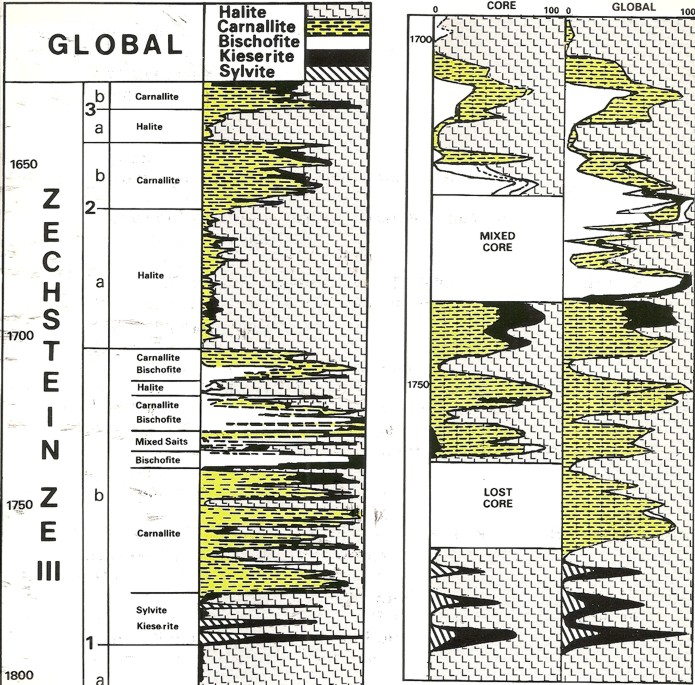
Modern logs from Germany run with a probabilistic analysis model.